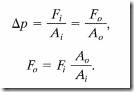Pascal’s Principle and the Hydraulic Lever

Demonstrating Pascal’s Principle

Consider the case in which the incompressible fluid is a liquid contained in a tall cylinder, as in figure :

The cylinder is fitted with a piston on which a container of lead shot rests. The atmosphere , container and shot exert pressure p_ext on the piston and thus on the liquid. The pressure p at any point P in the liquid is then

Let us add a little more lead shot to the container to increase p_ext by an amount The quantities rho, g and h in equation are unchanged , so the pressure change at P is

This pressure change is independent of h, so it must hold for all points within the liquid, as Pascal’s principle states.

Pascal’s Principle and the Hydraulic Lever

Figure showsn how pascal’s principle can be made the basis of a hydraulic lever. In operation, let an external force of magnitude F_i be directed downward on the left-hand ( or input) piston, whose surface area is A_i . An incompressible liquid in the device then produces an upward force of magnitude F_o on the right-hand ( or output ) piston, whose surface area is A_o . To keep the system in equilibrium , thre must be a downward force of magnitude F_o on the output piston from an external load ( not shown ) . The force F_i applied on the left and the downward force F₀ from the load on the right produce a change p in the pressure of the liquid that is given by

Equation shows that the output force F₀ on the load must be greater than the input force F_i if A₀ > A_i , as is the case in Figure.

If we move the input piston downward a distance d_i , the output piston moves upward a distance d₀ , such that the same volume V of the incompressible liquid is displaced at both pistons. Then

Which we can write as

This shows that , if A₀ > A_i the output piston moves a smaller distance than the input piston moves. We can write the output work as

Which shows that the work W done on the input piston by the applied force is equal to the work W done by the output piston in lifting the load placed on it. The advantage of a hydraulic lever is this :

“ With a hydraulic lever, a given force applied over a given distance can be transformed to a greater force applied over a smaller distance.

The product of force and distance remains unchanged so that the same work is done. However, there is often tremendous advantage in being able to exert the larger force. Most of us, for example , cannot lift an automobile directly but can with a hydraulic jack, even though we have to pump the handle farther than the automobile rises and in a series of small strokes.